MATH 112 Week 9 Final Exam | Assignment Help | Embry Riddle Aeronautical University
- embry-riddle-aeronautical-university / MATH 112
- 09 Oct 2019
- Price: $30
- Other / Other
MATH 112 Week 9 Final Exam | Assignment Help | Embry Riddle Aeronautical University
1. Evaluate.
∫x2−9x+2 dx
2. Find
the area under the given curve over the indicated interval.
y =
x2 [1, 2]
Area
=∫ x2 dx [1, 2]
3. y
= 2x3 – 24x – 2
dy/dx = 6x2
– 24
4. Find
the equation of the curve that passes through (2,3)if its slope is given by the following
equation
dy/dx = 3x – 4
Slope at x = 2 3*2 – 4 =
6 – 4 = 2
5. f(x)
= 2/3x a = 2, b = 3 n = 2
∆x
= (3 – 2) /2 = ½ = 0.5
So
Intervals are 2, 2.5, 3
6.
x = t(2t + 1)2
y = 5/ √5t + 5
Find the magnitude and direction of the
velocity when t = 0.25
7.
Antiderivative f(x) = 9/x3+ 1/82
8. Evaluate
the given definite integral.
9.
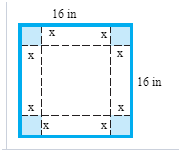
An
open box is to be made from a square piece of cardboard whose sides are 16 inches long, by cutting squares of
equal size from the corners and bending up the sides. Determine the size of the
square that is to be cut out so that the volume may be a maximum.
10.
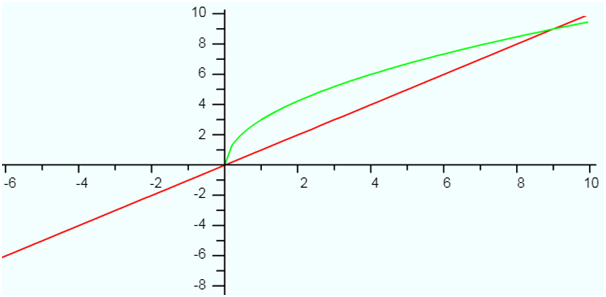
y
= x
Y = 3√x
Graph is like this
11.
A
rocket follows a path given by y = x -
1/75 x3(distances in miles). If the horizontal velocity
is given by
vx
= x
find the magnitude and direction of the velocity when the rocket hits
the ground (assume level terrain) if time is in minutes.
Magnitude
of the velocity of the rocket at the point
Find
the direction of the velocity of the rocket at the point Enter an angle θsuch
that 0 degrees less than or equals theta less than 360 degrees .0°≤θ<360°.
Select the correct choice below and fill in any answer boxes in your choice.
12.
The
height (in ft) of a flare shot upward from the ground is given by S = 89.6
t – 16t2
where
t is the time (in s). What is the greatest height to which the
flare goes?
Find
the derivative of the function to be maximized.

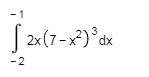






 USA
USA  India
India
Question Attachments
0 attachments —